1.5 谐波

“谐波”这一术语与波形的基本频率有关。在学习谐波之前，我们应该熟悉一些波形的概念。让我们讨论自然频率和强迫频率这两个主题。

不同谐波频率

自然频率

当一个物体在没有任何外力作用下自由振动时，这种振动被称为“自然振动”。自然振动发生的频率被称为“自然频率”。

强迫频率

当一个物体在外力周期性作用下振动时，这种振动被称为“强迫振动”。强迫振动的频率被称为“强迫频率”。

行波

当一个波在介质中持续向前传播，且在路径的任何点都不会被反射时，这种波被称为“行波”。

驻波

当两个频率和振幅相同的行波在介质中朝相反方向传播时，它们会相互叠加。这种叠加后的波被称为“驻波”。在驻波中，我们可以找到节点和反节点。

基本频率

基本频率被定义为周期性波形的最低频率。它通常用 $f$ 表示。换句话说，一个振动物体的最低共振频率被称为“基本频率”。

什么是谐波？

谐波是一个频率，它是基本频率的整数倍。一个物体的强迫共振振动会导致产生驻波。在自然频率下，它形成了驻波模式。这些模式是在特定频率下产生的，被称为“谐波频率”或“谐波”。

在谐波频率下产生的声音非常清晰，而在其他频率下，我们得到的是噪声，无法听到清晰的波形声音。

谐波可能出现在任何形状的波形中，但它们主要出现在正弦波中。非正弦波形，如三角波和锯齿波，是通过将谐波频率相加来构建的。通常，“谐波”一词被用来描述由不同不期望的频率引起的正弦波的失真，这些频率被称为“噪声”。

在每一个谐波中，我们都可以找到两个位置，它们是节点和反节点。

节点

节点是沿着介质看起来静止不动的点。它们没有位移。因此，它们也被称为节点。

反节点

反节点是两个节点之间发生最大位移的粒子。这里的一个节点是正的，另一个是负的。节点和反节点如下图所示。

节点和反节点出现在波形中。因此，波形具有谐波频率。基本频率是谐波中的最低频率。因此，在它们之间只出现一个反节点。这个反节点是两个节点的中间。因此，我们可以得出结论，吉他弦产生最长的波长和最低的频率。

任何乐器产生的最低频率被称为基本频率。这也可以被称为波的“第一谐波”。用基本频率的话来说，谐波是基本频率的整数倍。

例如：$f, 2f, 3f, 4f$ 等等都是谐波。

由于基本频率的多个整数倍，我们将有无数个谐波，如第一谐波、第二谐波、第三谐波等。

第一谐波

正如我们之前讨论的，基本频率也被称为第一谐波。在第一谐波中，我们有两个节点和一个反节点。

第二谐波

第二谐波包含三个节点和两个反节点。如果我们在第一谐波的两个节点之间设置一个节点，我们就可以得到第二谐波。在第一谐波中，第二个节点将位于两个节点之间，即第一个和最后一个。

第三谐波

对于第三谐波，如果在弦的两端各放置一个节点，得到的波形模式包含四个节点和三个反节点。这意味着第三谐波的波形有一个完整的正弦波周期和半个周期。图表如下所示。

通过观察上述讨论，我们可以得出结论，反节点的数量等于特定谐波的整数倍。也就是说，第一谐波有一个反节点，第二谐波有两个反节点，等等。

谐波频率的计算

谐波频率可以通过以下公式计算：

$\text{速度} = \text{频率} \times \text{波长}$ $V = n \times \lambda$ $n\text{次谐波} = n \times \text{基本频率}$

如果我们知道波形的速度和波长，我们就可以计算谐波频率。波中有两种类型的谐波，它们是偶次谐波和奇次谐波。例如，一个两端都开放的圆柱体将在偶次和奇次谐波下振动，但一个有一端封闭的圆柱体将只在奇次谐波下振动。

谐波的特性

我们听到的大多数振动都是由谐波引起的。例如，吉他、小提琴甚至人声的音乐声音。谐波也被称为谐波分量。谐波的特性取决于乐器或波形的振动。

因此，一般来说，振动是产生谐波的原因。振荡器不过是一个移动或振动的乐器。部分谐波会产生与全谐波不同的频率。但是，长长度和细线的乐器会产生精确的谐波频率。

它们只产生一个精确的谐波。在基本频率的整数倍下出现的频率被称为谐波频率。

人耳无法清晰地听到所有谐波。非谐波频率的频率被称为非谐波频率。在这里，许多谐波结合在一起形成声音。非谐波声音对人耳是可听的。

例如：第一，我们经常看到的学校铃声和教堂铃声。第二，古董唱碗是其他只在谐波频率下振动的例子。谐波的一个重要特性是，所有谐波在基本频率下都是周期性的，然后谐波的总和也在基本频率下是周期性的。

谐波和泛音

高于基本频率的频率被称为“泛音”。一般来说，泛音存在于乐器中。泛音取决于乐器的音调。由于音调会因乐器而异，泛音的发生也会有所不同。通过混合/组合泛音，我们可以获得乐器的基本音调。

观察上述不同乐器（小提琴和钢琴）产生的声音输出。它们具有相同的频率，因此它们具有相同的音符，它们的泛音不同，最终它们的声音也不同。这意味着乐器的泛音可以影响其声音输出。小提琴的锯齿波形表示更尖锐的声音，而钢琴产生更纯净的声音，更接近正弦波。

长度与波长的关系

为了得到长度和波长的关系，我们再次观察所有谐波。即第一、第二、第三谐波。我们都知道正弦波的波长是“lambda”。谐波也被表示为正弦波。让我们计算

从第一谐波来看，在第一谐波中，弦的两端是固定的，它们被称为节点。当有振动时，导线上下移动，形成一个反节点。因此，这个图形像一个半正弦波。因此，波长的一半

从第二谐波来看，第二谐波中有两个反节点，因此有两个环。从第一谐波我们已经计算出一个环等于半个波长。因此，这里有两个环，总共一个波长。

从第三谐波来看，在第三谐波运动中有三个环，每个环包含半个波长。因此，所有三个环的总和是 $\frac{3}{2}$ 个波长。

从所有这些谐波来看，我们可以得出结论，对于第一谐波，我们有一个反节点，对于第二谐波有两个反节点，对于第三谐波有三个反节点。因此，对于第 $n$ 次谐波，有 $n$ 个反节点。

因此，通过推导长度和波长关系的公式，我们得到

$L = \frac{n}{2} \text{波长}$

我们也可以将这些公式写成如下形式

对于第一谐波：$L = \frac{1}{2} \lambda$

对于第二谐波：$2L = \lambda$

对于第三谐波：$3L = \frac{3}{2} \lambda$

对于第 $n$ 次谐波：$nL = \frac{n}{2} \lambda$，其中 $n$ 是一个整数。

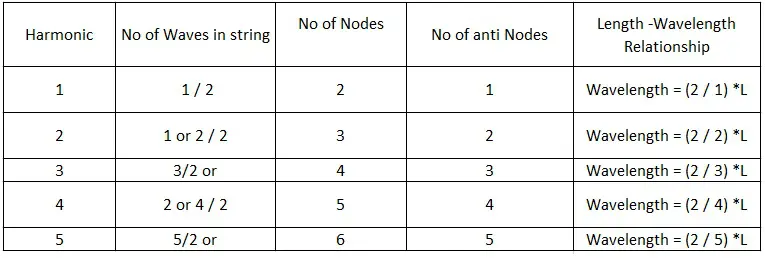
长度与波长的关系在谐波中的数学关系如下表所示

$L = \frac{n}{2} \lambda$

谐波的缺点

谐波会影响电力系统的性能。谐波的缺点如下：

• 谐波会降低配电网络中电力供应的质量，可能会导致多种负面影响。
• 谐波可能会增加有效的均方根（RMS）电流，从而导致配电系统的功率损失。
• 第三次谐波的累积增加可能会导致中性导体过载。
• 谐波会增加电信号的噪声水平。
• 谐波可能会干扰供电电压，从而导致敏感负载的错误操作。
• 谐波会在通信线路和电话线路中引起干扰。
• 谐波会影响供电电感与功率因数电容器的电容水平之间的谐振。

简而言之，谐波会在电力系统和电信系统中引起以下问题：

• 设备发热
• 设备功能异常
• 设备故障
• 通信干扰
• 熔断器和断路器误动作
• 工艺问题
• 导体发热

谐波示例

我们已经知道，在日常生活中我们会遇到许多谐波频率，这里我们来看一些谐波的例子。

示例

许多振荡器，如拨动的吉他弦，会在许多频率下振动，但这些并非谐波，通常被称为部分谐波。因此，当我们取一个细长的振荡器时，频率会出现在谐波范围内。为了确定谐波发生的确切位置，我们首先需要计算波形的基本频率。

让我们以一根产生谐波频率的吉他弦为例。将弦的两端固定并安装在吉他结构中，这样两端就无法移动。我们已经知道，谐波波是由驻波产生的，它们有节点和反节点。

在这种情况下，两端都是节点，因此存在反节点。因此，本身就存在一个谐波频率。基本频率是最低的频率，因此在它们之间有一个反节点。这个反节点位于两个节点的中间。因此，我们可以得出结论，吉他弦产生最长的波长和最低的频率。

任何乐器产生的最低频率被称为基本频率，也称为第一谐波。